Disclaimer. The codes and articles provided here are intended for personal use only. You are welcome to use and modify the codes with proper reference. Files downloaded from this webpage are not permitted to be uploaded to any public server, or be distributed for any commercial purpose without written permissions from the authors.
Rigidly and Flat-Foldable Quadrilateral Origami
The code aims to design rigidly and flat foldable quadrilateral origami. This concept involves the use of geometric principles to create complex shapes from initially flat sheets of material. The design and deformations of all possible rigidly and flat-foldable quadrilateral mesh origami are characterized, with a focus on the compatibility of crease patterns and the development of an inverse problem to design crease patterns for targeted shapes.
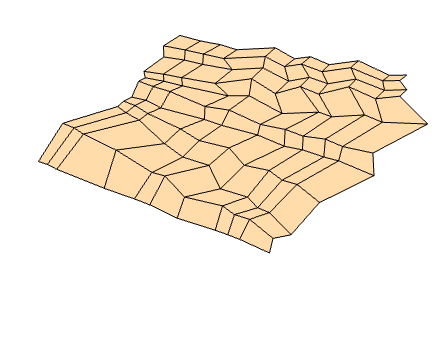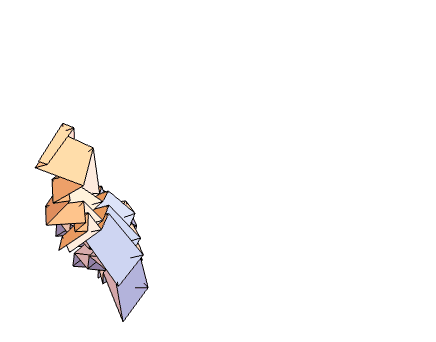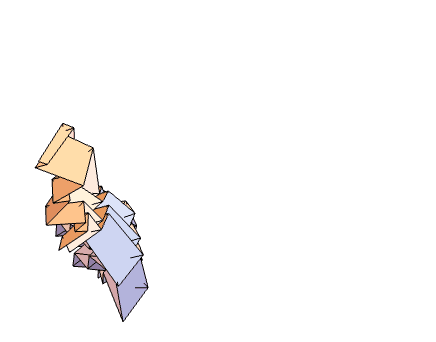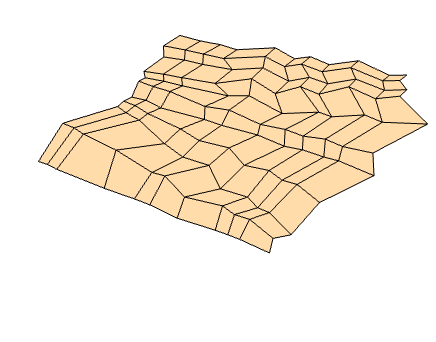

Left: Generic rigidly and flat-foldable quadrilateral mesh origami; Right: Inverse design of an origami curved surface.
Download Code | Download Article
References:
F. Feng, X. Dang, R. D. James, and P. Plucinsky. The designs and deformations of rigidly and flat-foldable quadrilateral mesh origami. Journal of the Mechanics and Physics of Solids , pp. 104018, 2020.
X. Dang, F. Feng, P. Plucinsky, R. D. James, H. Duan, and J. Wang. Inverse design of deployable origami structures that approximate a general surface. International Journal of Solids and Structures 234, pp. 111224, 2022.
Deployable Quadrilateral Kirigami
This research presents a unified design method for deployable quadrilateral kirigami tessellations with different topologies. The method is based on the parametrization of kirigami patterns, formulated as the solution of a linear equation system. The geometric constraints for deployability are covered by a unified theorem, allowing for the design of kirigami tessellations that achieve desired shapes while preserving the topological characteristics of the flat sheets.


Left: Deployable planar quadrilateral kirigami; Right: Bistable spherical quadrilateral kirigami.
Download Code | Download Article
References:
X. Dang, F. Feng, H. Duan, and J. Wang. Theorem for the design of deployable kirigami tessellations with different topologies. Physical Review E 104, pp. 055006, 2021.
X. Dang, F. Feng, H. Duan, and J. Wang. Theorem on the compatibility of spherical kirigami tessellations. Physical Review Letters 128, pp. 035501, 2022.
Morphoshell
Morphoshell is a computational tool for simulating the shape transformations in active materials and structures. It allows for the exploration of shape-morphing capabilities of materials like liquid crystal elastomers and can be used to design and analyze structures that respond to external stimuli. The software provides a platform for both research and practical applications in the field of soft matter and mechano-responsive materials.
Morphoshell was developed by Dr. Daniel Duffy and Dr. John Biggins at Cambridge University.
Dr. Daniel Duffy: https://www.danielduffy.org/
Dr. John Biggins: https://www.soft.eng.cam.ac.uk/


Left: Actuation of a nematic elastomer flat sheet encoded with an m=-2 defect. Video courtesy of Daniel Duffy; Right: Actuation of a Gaussian grabber.
References:
D. Duffy and J. S. Biggins, Defective nematogenesis: Gauss curvature in programmable shape-responsive sheets with topological defects, Soft Matter, 16,
10935–10945 (2020).
F. Feng, K. Dradrach, M. Zmyslony, M. Barnes, and J. S. Biggins, Geometry, mechanics and actuation of intrinsically curved folds, Soft Matter, 20(9), 2132-2140 (2024).
Surface Instability


Left: Surface sulci in squeezed soft solids; Right: Liquid crystal elastomer (LCE) surface instability under compression.
References:
T. Tallinen, J. S. Biggins, and L. Mahadevan, Surface sulci in squeezed soft solids, Phys. Rev. Lett. 110, 024302 (2013).
M. Barnes, F. Feng, and J. S. Biggins, Surface instability in a nematic elastomer, Phys. Rev. Lett. 131, 238101 (2023).