Phase transformation and its applications
Martensitic phase transformation in crystalline solids is a first-order, solid to solid, diffusionless phase transformation. The structure exhibits changes in symmetry groups and structural parameters at the phase transformation temperature. We study phase transformation theories under various symmetry groups, including translational and helical groups. Incorporating the geometrical compatibility, we design advanced phase-change materials that have fruitful microstructures and cycling lifetime. Meanwhile, physical properties such as ferroelectricity and ferromagnetism also change during the phase transformation. Thus, we could use these materials in the environment friendly elastocaloric/magnetocaloric cooling.

(a) Martensitic phase transformation in crystals. (b) Phase transformation in helical structures [2]. (c) Elastocaloric cooling. Image courtesy of Dr. Jingyuan XU at KIT, Germany.
Origami and kirigami structures
Origami is an ancient art form of paper folding. From the mathematical point of view, an origami pattern with arbitrary crease distribution is an over constrained system, if we assume the panels are rigid and can only rotate around the creases. Thus, designing an origami pattern that is rigidly foldable (the panels are not bent nor stretched) is a challenging task.
We rigorously solve the deployability problem for a family of origami structures, namely rigidly and flat foldable quadrilateral mesh origami [4][9], by solving geometrical compatibility equations for folding angles. As shown in the video, the origami can be folded from a flat state to a folded-flat state. Mirua origami is an example. Owing to its non-linear feature, an optimal shape of intermediate state can be designed and used as robots and actuators. Surprisingly, we find similar results in quadrilateral krigami systems [8][11], where opening angle functions serve as key terms in geometric compatibility equations.
Liquid crystal elastomers
Liquid crystal elastomers (LCEs) are active soft materials that can have significant shape changes upon heat or illumination. Microscopically, LCEs are networks of LC polymers. Actuation occurs via the isotropic-nematic phase transition, which biases conformations along the director, generating large elongations on cooling, and muscular contraction on heating.
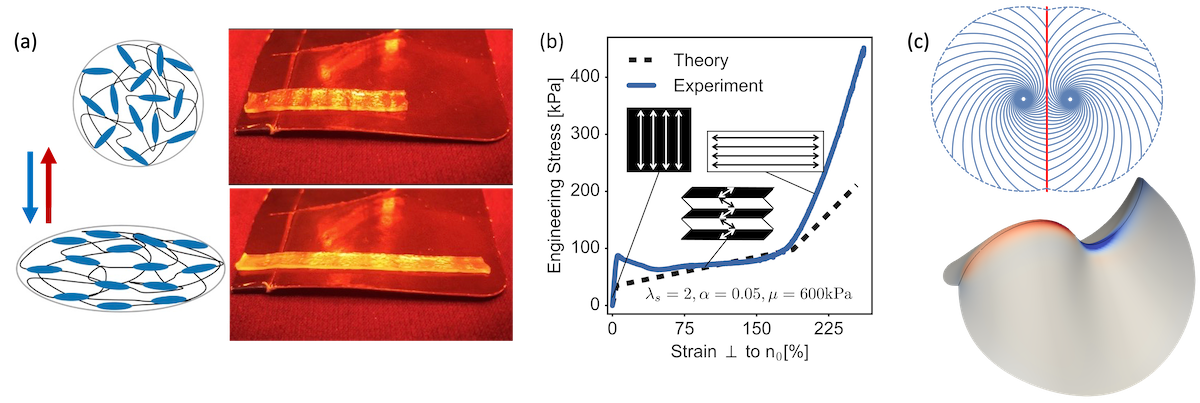
Liquid crystal elastomers (LCEs). (a) Phase transformation in LCEs. (b) Semi-soft elasticity [15]. (c) Shape programming [13][17].
Built upon the phase transformation in LCEs, two main topics arise: abnormal mechanics due to soft elasticity and shape programming based on director distribution. Soft elasticity is the result of rearrangement of Goldstone-like ‘soft modes’ in which deformations induce director rotation at almost zero energy. This will regulate the constitutive relation and result in different mechanical responses. In shape programming, elongation and contraction define a metric corresponding to the director orientation in 2D LCE sheets. Thus we may design the director orientation to achieve desired mechanical and geometric properties such as Gaussian curvature.
Data-driven/AI aided design of advanced materials and structures
Harnessing the power of big data/AI, we aim to design phase-changing materials that have outstanding cycling life time and porous structures that can enhance the efficiency of thermal conductivity in elastocaloric cooling.
